T-SNE - T-distributed Stochastic Neighbor Embedding

What is T-SNE ?

Different with PCA, T-SNE is a non-linear technique.
Different with PCA, T-SNE CANNOT be reused for new data. It is only used for data exploration.
- Because - “t-SNE has a cost function that is not convex, i.e. with different initializations we can get different results.”
Perplexity is a target number of neighbors for the central point. Normally 5~50 i.e. how large is the “circle”

Resources

visualized t-SNE effect by different graph - https://distill.pub/2016/misread-tsne/
A post explained in Chinese - https://mropengate.blogspot.com/2019/06/t-sne.html
Guide on Medium - https://towardsdatascience.com/an-introduction-to-t-sne-with-python-example-5a3a293108d1
- Too complicated explanation for people without statistic background(like me…)
Another guide on medium - https://towardsdatascience.com/t-sne-clearly-explained-d84c537f53a
- A lot more chart, visual guide, simplified equation, easier to understand

Usage:

Implement with scikit - https://scikit-learn.org/stable/modules/generated/sklearn.manifold.TSNE.html#sklearn.manifold.TSNE
A guideline post about t-SNE - https://builtin.com/data-science/tsne-python

How to implement ?

Assumption:

It is good to visualize high dimensional data, BUT we need to reduce the dimension by ourselves as a preprocess. So that the dimension is less than a small number like 50
- e.g. apply PCA before inputting the data into TSNE
The number of sample cannot be too large, otherwise the memory/computation time explode

Implementation:

It can be as easy as:

from sklearn.manifold import TSNE

X_embedded = TSNE(n_components=2, learning_rate='auto',
                  init='random', perplexity=20).fit_transform(flat_x)
X_embedded.shape

How it works ?

From the guide on medium, its visualization is great:

1st step :

For each data points, generate a normal distribution with this point as the mean.

And the Euclidean distance as the x-axis in distribution

(Note that the distribution is not exactly like this in t-SNE, here is simplified for explanation)

Untitled

The original distribution should be like this : (img also from medium post)

Untitled

2nd Step :

Create a new & low-dimension space.

Put all the data points randomly on this space

Like in 1st step, for each point create a Student t-distribution with a single degree of freedom

3rd Step : Gradient descent

To optimize the distribution from above (because we put the points randomly),

Kullback-Leibler divergence is used, between the 2 distribution we created.

This gradient help to “move” the point to its suitable position

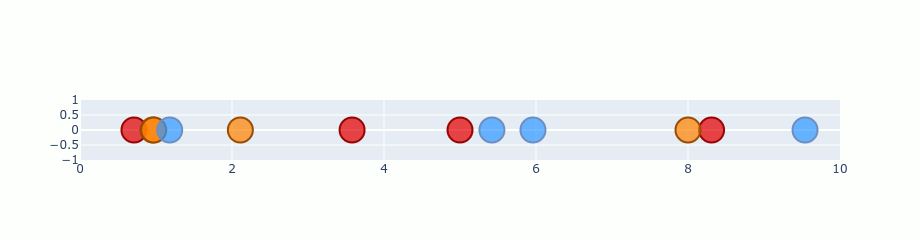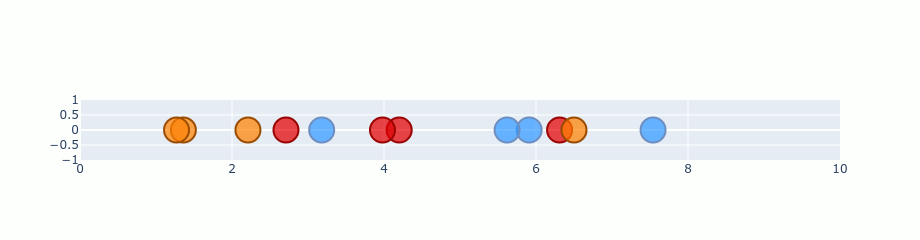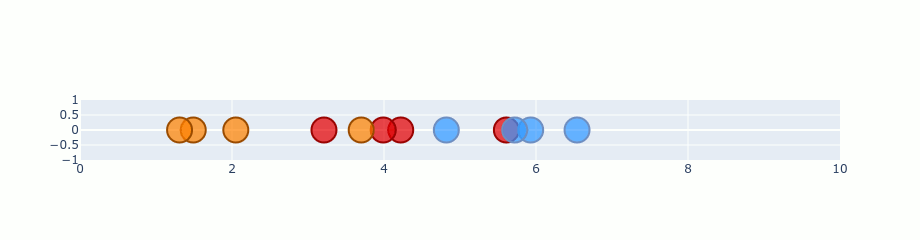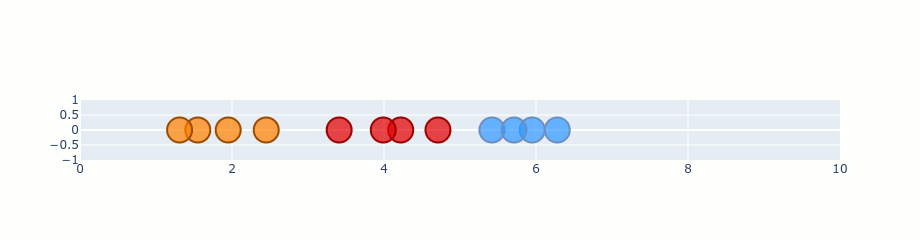
Usage Example :

For visualizing & exploring parameters inside a CNN network, that always seems a blackbox, because its parameters in hidden layers are too high-dimensional.

But t-SNE can be used here to visualize the parameters.